Exercícios
O número de soluções disponíveis é relativamente pequeno. Poderá querer consultar a versão anterior.
Integração
- (Exercício VI.1 de [1]) Considere a função $f$ definida no intervalo $[0,2]$ por \[ f(x)=\begin{cases} 1 &\text{ se } x\in [0,1[,\\ 2 &\text{ se } x=1,\\ 3 &\text{ se } x\in{]1,2]}. \end{cases} \]
- Mostre que para toda a decomposição do intervalo $[0,2]$, as somas superior $S_d(f)$ e inferior $s_d(f)$ verificam $s_d(f)\leq 4\leq S_d(f)$.
- Recorrendo directamente à definição, mostre que $f$ é integrável e que $\int_0^2f(x)dx =4$.
-
- Sendo $f:[a,b]\to\mathbb{R}$ uma função integrável, mostre que $f^2$ é integrável.
Sugestão
Considere $f\geq 0$; o caso geral segue de $f^2=|f|^2$.
Solução
Seja $f\geq 0$. Para cada decomposição $d=\{a=t_0, t_1,..., t_n=b\}$, temos \[M_i(f^2)=\sup_{x\in[t_{i-1},t_i]}f^2(x)=\left(\sup_{x\in[t_{i-1},t_i]}f(x)\right)^2=M_i(f)^2,\] \[ m_i(f^2)=\inf_{x\in[t_{i-1},t_i]}f^2(x)=\left(\inf_{x\in[t_{i-1},t_i]}f(x)\right)^2=m_i(f)^2.\]
Temos então \begin{align*} S_d(f^2)-s_d(f^2)& =\sum_{i=1}^n (M_i(f^2)-m_i(f^2))(t_i-t_{i-1})\\ & = \sum_{i=1}^n (M_i(f)^2-m_i(f)^2)(t_i-t_{i-1})\\ & = \sum_{i=1}^n (M_i(f)-m_i(f)) (M_i(f)+m_i(f))(t_i-t_{i-1})\\ & \leq 2M \sum_{i=1}^n (M_i(f)-m_i(f))(t_i-t_{i-1})=2M( S_d(f)-s_d(f)), \end{align*} onde $M=\sup_{x\in[a,b]}f(x)$. Dado $\epsilon>0$ arbitrário, como $f$ é integrável, podemos escolher a decomposição $d$ de maneira a $S_d(f)-s_d(f)\lt \frac{\epsilon}{2M}$, e portanto \[ S_d(f^2)-s_d(f^2)\lt \epsilon.\]
Conclui-se que $f^2$ é integrável para $f\geq 0$ integrável.
Para $f$ arbitrária, usamos que sabemos que então $|f|$ é integrável e usamos $f^2=|f|^2$.
- Sendo $f:[a,b]\to\mathbb{R}$, $g:[a,b]\to\mathbb{R}$ integráveis, justifique que $fg$ á integrável.
Sugestão
$fg=\frac{1}{2}((f+g)^2-f^2-g^2)$.
Solução
De $fg=\frac{1}{2}((f+g)^2-f^2-g^2)$, temos que $fg$ é uma combinação linear de funções integráveis, e portanto integrável.
- Sendo $f:[a,b]\to\mathbb{R}$ uma função integrável, mostre que $f^2$ é integrável.
- (Exercício VI.3 de [1]) Prove que, se $f$ é contínua em $[a,b]$ ($a\leq b$) e $g$ é integrável e não negativa em $[a,b]$, existe $c\in[a,b]$ tal que \[\int_a^bf(x)g(x)dx=f(c)\int_a^bg(x)dx.\]
- (Exercício VI.7 de [1]) Mostre que se $f$ é contínua em $[a,b]$ ($a\lt b$) e $\int_a^b f(x)dx=0$, existe pelo menos uma raiz da equação $f(x)=0$ no intervalo $[a,b]$.
-
(Exercício 6.10 de [2]) Sendo $f$ uma função contínua em $\mathbb{R}$, prove que se é nulo o integral de $f$ em qualquer intervalo limitado, então $f(x)=0$, para qualquer $x\in\mathbb{R}$.
Dê um exemplo de uma função integrável e com integral nulo em qualquer intervalo limitado e que não verifique $f(x)=0$ para qualquer $x\in\mathbb{R}$.
- (Exercício 6.13 de [2]) Calcule $\phi'(x)$ sendo $\phi(x)=\int_x^3 x^2e^{\sen t}\,dt$.
- Determine as derivadas das funções seguintes:
- $\int_{1}^{x}\sen(t^{2})\,dt$.
- $\int_{x}^{2\pi}\cos(t^{2})\,dt$
- $\int_{x}^{2x}e^{t^{2}}\,dt$.
- $\int_{x}^{x^{2}}e^{-t^{2}}\,dt$.
- $\int_{x^{2}}^{x^{4}}\sen (\sqrt{t})\,dt$.
- Seja $f:\mathbb{R}\to \mathbb{R}$ uma função contínua e $\psi(x)=\int_0^x(x-t)f(t)dt$. Justifique que $\psi$ é duas vezes diferenciável e calcule $\psi''(x)$.
- (Exercício 6.9 de [2]) Mostre que se $f$ é uma função diferenciável em $\mathbb{R}$ verificando a condição \[\int_0^x f(t)\,dt=xf(x),\qquad \forall x\in\mathbb{R}\] então $f$ é uma função constante.
Sugestão
derive ambos os membros da igualdade anterior.
- Mostre que a função seguinte não depende de $x$: \[\psi(x)=\int_{-\cos x}^{\sen x} \frac{1}{\sqrt{1-t^2}}\, dt,\quad x\in\left]0,\frac{\pi}{2}\right[.\]
- (Exercício 6.16 de [2]) Calcule \[ \lim_{x\to 0}\frac{\int_0^{x}\sen t^3\,dt}{x^4}. \]
- Calcule os limites:
- $\lim_{x\to+\infty}x\int_{\pi/2}^{\arctg x}\sen(t^2)\,dt$.
- $\lim_{x\to 0^+}\frac{\int_0^{x^2}te^{\sqrt{t}}\,dt}{\int_0^{x^3}(e^{\sqrt[3]{t}}-1)\,dt}$.
- $\lim_{x\to 0^+} \frac{\int_0^{x} (e^{t^2}-t-1)\, dt}{\int_0^{x}\sen(t^2)\, dt}$.
- Calcule $\displaystyle \lim_{x\to +\infty}\dfrac{\int_0^{x^2}e^{t^2}\, dt}{\int_0^{x}t^2e^{t^2}\, dt}$.
Solução
Note-se que para $x\geq 1$ temos $\int_0^{x^2}e^{t^2}\, dt \geq \int_0^{x^2}1 \, dt=x^2 \to +\infty$ e $\int_0^{x}t^2e^{t^2}\, dt\geq \int_1^x e\, dt = (x-1)e \to +\infty$ de maneira que para resolver a indeterminação $\frac{\infty}{\infty}$ usamos nomeadamente a regra de Cauchy, o teorema de derivação da função composta e o teorema fundamental do cálculo para obter \begin{align*}\lim_{x\to +\infty}\frac{\int_0^{x^2}e^{t^2}\, dt}{\int_0^{x}t^2e^{t^2}\, dt} & = \lim_{x\to +\infty} \frac{2x e^{x^4}}{x^2 e^{x^2}} \\ & = \lim_{x\to +\infty} \frac{2 e^{x^4-x^2}}{x} \\ & = \lim_{x\to +\infty} (8x^3-4x) e^{x^4-x^2} = +\infty.\end{align*}
- (Exercício 6.53 de [2]) Seja $f$ uma função contínua em $\mathbb{R}$ e tal que $f(x)\gt 0$ para qualquer $x\in\mathbb{R}$ e $F(x)=\int_0^xf(t)\,dt$.
- Justifique que $F$ é diferenciável em $\mathbb{R}$ e calcule $F'(x)$.
- Mostre que $F$ é estritamente crescente e que, para $x\in \mathbb{R}\setminus\{0\}$, $xF(x)\gt 0$.
- Prove que se $f$ tem limite positivo quando $x\to +\infty$, então $\lim_{x\to +\infty} F(x)=+\infty$. Mostre, por meio de exemplos, que se for $\lim_{x\to+\infty}f(x)=0$, então $\lim_{x\to +\infty} F(x)$ pode ser finito ou $+\infty$.
- (Exercício 6.46.c) de [2]) Seja $f$ uma função contínua em $\mathbb{R}$ e \[ F(x)=\begin{cases} \frac{1}{x}\int_0^xf(t)\,dt, &\text{ se } x\neq 0,\\ f(0), &\text{ se }x=0.\end{cases}\] Prove que $F$ é contínua em $\mathbb{R}$ e diferenciável em $\mathbb{R}\setminus\{0\}$; mostre que, nas condições indicadas, $F$ pode não ser diferenciável em $0$.
- (Exercício VI.15 de [1]) Sejam $u$ e $v$ funções contínuas em $\mathbb{R}$ e tais que, para cada $x\in\mathbb{R}$: \[ \int_a^xu(t)\,dt=\int_b^xv(t)\,dt, \] onde $a,b\in\mathbb{R}$. Mostre que $u=v$ e $\int_a^bu(t)\,dt=0$.
-
Sejam $f:\mathbb{R}\to \mathbb{R}$ e $g:\mathbb{R}\to \mathbb{R}$ duas funções integráveis em qualquer intervalo limitado e a seguinte propriedade: \begin{align} \int_{-x}^{x}f(t)\,dt & = 2 \int_{0}^{x}f(t)\,dt\quad \forall x\in\mathbb{R}, \label{1imparpar}\\ \int_{-x}^{x}g(t)\,dt & = 0 \quad \forall x\in\mathbb{R}. \label{2imparpar} \end{align}
- Mostre que se $f$ é par e $g$ é ímpar então verificam $(\ref{1imparpar}, \ref{2imparpar})$.
- Mostre que se $f$ e $g$ são contínuas e verificam $(\ref{1imparpar}, \ref{2imparpar})$ então $f$ é par e $g$ é ímpar.
- Forneça exemplos de funções $f$ e $g$ que verificam $(\ref{1imparpar}, \ref{2imparpar})$ e que não sejam par nem ímpar, respectivamente.
- Calcule
- $\int_{1}^{2}\frac{1}{x}\,dx$,
- $\int_{-2}^{-1}\frac{1}{x}\,dx$,
- $\int_{-1}^{1}\sqrt[3]{x}\, dx$,
- $\int_{-1}^1\tg x\,dx$.
- Calcule
- $\int_\frac{1}{2}^1\log x\, dx$,
- $\int_{0}^{1}\frac{1}{(x+1)^{2}}\arctg x\,dx$,
- $\int_{0}^{1}\log(1+\sqrt{x})\,dx$,
- $\int_{0}^{\pi/3}\frac{\sen 2x}{1+\sen^{4}x}\,dx$,
- $\int_ 0^\frac{\pi}{4}\frac{\cos x}{\sen x +\cos x}\,dx$,
- $\int_{-2}^{-1}\frac{1}{x^2+4x+5}\,dx$,
- $\int_{0}^{\pi/3}\frac {8\tg x}{ 1+\sen^{2}x}\,dx$.
- (Inclui exercícios 6.23, 6.24, 6.26, 6.32 de [2]) Calcule
- $\int_1^\pi x\arctg x\,dx$,
- $\int_0^1 \frac{\arctg x}{1+x^2}\,dx$,
- $\int_0^\pi \sen^3x\,dx$,
- $\int_0^1 \frac{1}{x-3}\,dx$,
- $\int_2^4 \frac{x^3}{x-1}\,dx$,
- $\int_0^1 \frac{1}{e^t+ e^{2t}} \,dt$.
- $\int^{\log 2}_{0}\,\frac{e^t+1}{e^{2t}+1}\,dt$.
- $ \int^{1}_{0}\frac{e^{3x}}{1+e^{x}}\,dx$.
Solução
Considerando a substituição $u=e^x$ obtém-se \begin{align*} \int^{1}_{0}\frac{e^{3x}}{1+e^x}\,dx & = \int_1^{e} \frac{u^3}{1+u} \frac{1}{u}\, du = \int_1^{e} \frac{u^2}{1+u} \, du \\ &= \int_1^{e} u-1 + \frac{1}{1+u} \, du = \left.\left[\frac{u^2}{2}-u+\log|1+u|\right]\right|^e_1 \\ &= \frac{e^2}{2}- e+ \log(1+e)-\frac{1}{2}+1-\log2 \\ &=\frac{e^2}{2}- e+\frac{1}{2}+\log\frac{1+e}{2}. \end{align*}
- Calcule
- $\displaystyle\int_1^{\sqrt{3}}\frac{1}{(x^2+1)\arctg x}\, dx$.
Solução
\begin{align*}\int_1^{\sqrt{3}}\frac{1}{(x^2+1)\arctg x}\, dx & =\int_1^{\sqrt{3}}\frac{d}{dx} \left(\log\arctg x\right)\, dx \\ &= \log\arctg\sqrt{3}-\log\arctg 1 =\log\frac{\pi}{3}-\log\frac{\pi}{4}=\log 4 -\log 3.\end{align*}
- $\displaystyle\int_0^1e^{-x}\log(1+e^{2x})\, dx$
Solução
Considerando a substituição $u=e^x$ obtemos \[\int_0^1e^{-x}\log(1+e^{2x})\, dx = \int_1^e \frac{1}{u^2}\log(1+u^2)\, du.\] Continuando, integrando por partes, obtém-se \begin{align*}\int_1^e \frac{1}{u^2}\log(1+u^2)\, du & = \int_1^e \frac{d}{du}\left(-\frac{1}{u}\right)\log(1+u^2) \, du \\ & = \left.\left[-\frac{1}{u} \log(1+u^2) \right]\right|^e_1 + \int_1^e \frac{1}{u} \frac{2u}{1+u^2}\, du\\ & = -\frac{1}{e} \log(1+e^2) +\log 2 + 2\arctg e - \frac{\pi}{2} \end{align*}
- $\displaystyle\int_1^{\sqrt{3}}\frac{1}{(x^2+1)\arctg x}\, dx$.
- (Exercício V.9 de [1]) Sendo $F(x)=\int_1^x\frac{1}{t}e^{\frac{t^2+1}{t}}dt$, $x\gt 0$, mostre que \[F\left(\frac{1}{x}\right)=-F(x).\]
- Seja $f:\mathbb{R}^+\to\mathbb{R}$ uma função contínua. Define-se $F:\mathbb{R}^+\to\mathbb{R}$ através da expressão $F(x)=\int_{\frac{1}{x}}^{\frac{1}{x^2}}f(tx)\,dt$. Justifique que $F$ é diferenciável em $\mathbb{R}^+$, e mostre que \[ F'(x)=-\frac{1}{x^2}\left(xF(x)+\frac{1}{x}f\left(\frac{1}{x}\right)\right),\quad x\gt 0. \]
Sugestão
considere a mudança de variável $tx=y$.
- Mostre que, para qualquer $x\gt 0$, \[ \int_{1}^{x}\frac{1}{1+t^{2}}\,dt= \int_{1/x}^{1}\frac{1}{1+t^{2}}\,dt. \]
Sugestão
use uma substituição de variável adequada.
- Considere a função $F:\mathbb{R}\to \mathbb{R}$ definida por \[F(x)=\int_0^x e^{-t^2}\,dt.\] Mostre que \[\int_0^1 F(x)\,dx = F(1)-\frac{1}{2}+\frac{1}{2e}.\]
Sugestão
use integração por partes.
- (Exercício 6.45 de [2]) Uma função $f:\mathbb{R}\to\mathbb{R}$ diz-se periódica de período $T\gt 0$, sse $\forall{x\in\mathbb{R}}, f(x)=f(x+T)$. Mostre que, se $f$ é contínua e periódica de período $T\gt 0$, então
- $G(x)=\int_{x}^{x+T} f(t)\,dt$ é uma função constante em $\mathbb{R}$.
- Sendo $F$ uma primitiva de $f$, $F$ será também periódica de período $T$ sse $\int_{0}^{T} f(t)\,dt =0$.
- Determine o domínio, intervalos de monotonia e extremos locais das funções:
- $f(x)=\int_{0}^{x^2}e^{t^2}\,dt$,
- $g(x)=\int_{2}^{e^x}\frac{1}{\log t}\,dt$,
- $h(x)=\int_1^x(x-t)e^{t^2}\,dt$.
- Considere \[ \phi(x)=\int^{x^2}_{0}\,e^{-2\sqrt t}\,dt. \]
- Determine o domínio de $\phi$ e calcule a sua derivada.
- Determine, se existirem, os extremos locais e pontos de inflexão de $\phi$.
- Considere a função definida por \[g(x)=\int_x^{x^2} \frac{\sqrt{t}}{\sen t}\, dt.\]
- Mostre que $g$ está definida se $x\in {]0,\sqrt{\pi}[}$.
Solução
Se $x\in {\left]0,\sqrt{\frac{\pi}{2}}\right[}$ então $x^2\in {\left]0,\frac{\pi}{2}\right[}$, pelo que o intervalo de extremos $x$ e $x^2$ está contido em ${]0,\pi/2[}$. Portanto o intervalo de integração é limitado e fechado estando aí a função integranda definida e sendo contínua. Logo o integral existe e $g$ está de facto definida para todos os valores de $x$ em ${\left]0,\sqrt{\frac{\pi}{2}}\right[}$.
- Calcule $g'(x)$.
Solução
Usando o teorema de derivação da função composta, o teorema fundamental do cálculo, e a aditividade do integral relativamente ao intervalo de integração, obtemos \begin{align*}\frac{d}{dx} \int_x^{x^2} \frac{\sqrt{t}}{\cos t}\, dt &= \frac{d}{dx} \left( - \int_{1/2}^x\frac{\sqrt{t}}{\cos t}\, dt + \int_{1/2}^{x^2} \frac{\sqrt{t}}{\cos t}\, dt \right) \\ &= -\frac{\sqrt{x}}{\cos x} + 2x \frac{\sqrt{x^2}}{\cos (x^2)}.\end{align*}
- Mostre que $g$ está definida se $x\in {]0,\sqrt{\pi}[}$.
- Seja $h:{[0,+\infty[}\to\mathbb{R}$ uma função contínua, não negativa e tal que \[ \lim_{t\to+\infty}h(t)e^t=0.\] Mostre que $\lim_{x\to+\infty}\int_0^x h(t)\, dt$ existe em $\mathbb{R}$.
Solução
Como $ \displaystyle\lim_{t\to+\infty}h(t)e^t=0$, existe $\alpha\in\mathbb{R}$ tal que, para $t\gt \alpha$, $h(t)e^t\lt 1$. Então temos, para $t\gt \alpha$, $0\leq h(t)\lt e^{-t}$. Portanto \begin{align*}0 \leq \int_0^x h(t)\, dt &= \int_0^\alpha h(t)\, dt + \int_\alpha^x h(t)\, dt \\ & \leq \int_0^\alpha h(t)\, dt + \int_\alpha^x e^{-t}\, dt \\ & \leq \int_0^\alpha h(t)\, dt + (e^{-\alpha}- e^{-x}) \\ & \leq \int_0^\alpha h(t)\, dt + e^{-\alpha}.\end{align*} Assim verificamos que o integral indefinido de $h$ é uma função crescente (visto $h\geq 0$) limitada e consequentemente terá um limite finito quando $x\to +\infty$.
- Mostre que a função definida em $\mathbb{R}$ por \[g(x)=\int_{x^2}^{x^4}e^{-t^2}\, dt\] é uma função limitada.
Solução
Para $x\geq 1$: \[0\leq \int_{x^2}^{x^4}e^{-t^2}\, dt \leq \int_{x^2}^{x^4}\sup_{t\in[x^2, x^4]}e^{-t^2}\,dt \leq(x^4-x^2) e^{-x^4} \leq x^4 e^{-x^4}\leq \sup_{\lambda> 0}\lambda e^{-\lambda}= e^{-1}.\] (Atendendo a que \[ (\lambda e^{-\lambda})'=(1-\lambda)e^{-\lambda} \qquad \forall x\in\mathbb{R} \] facilmente se conclui da análise do sinal da derivada que a função $\lambda\mapsto \lambda e^{-\lambda}$ tem um máximo absoluto no ponto $x=1$.)
Dado que $g$ é função par, tem-se \[ 0\leq g(x)\leq e^{-1} \qquad \forall_{x:|x|\gt 1}. \] Como, além disso, a função $g$ é contínua em $\mathbb{R}$ (pelos teoremas da continuidade da função composta e da continuidade do integral indefinido), o teorema de Weierstrass garante que $g$ é limitada em $[-1,1]$ (ou, em alternativa de uma forma mais prosaica, note que com $x\in [-1,1]$ temos $-\int_0^1 e^{-t^2} \, dt \leq \int_{x^2}^{x^4} e^{-t^2} \, dt\leq 0$).
Assim, $g$ é uma função limitada em $\mathbb{R}$.
-
Seja $h:\mathbb{R}\to\mathbb{R}$ uma função contínua. Definindo \[g(x)=\int_0^x h(t-x)\, dt,\] justifique que $g$ é diferenciável em $\mathbb{R}$ e relacione a sua derivada com a função $h$.
Solução
Começamos por notar que a função integranda depende de $x$ o que impossibilita aplicar directamente o teorema fundamental do cálculo. No entanto podemos integrar por substituição para obter um integral em que não há dependência de $x$ na função integranda. Assim, consideramos a mudança de variável $u=t-x$ para obter $g(x)=\int_{-x}^0 h(u)\, du$. Para esta representação de $g$ já é lícito aplicar o teorema fundamental do cálculo e o teorema de derivação da função composta para obter $g'(x)=h(-x)$.
- Considere a função \[ f(x)= \begin{cases} \frac{e^{2x}-e^{x}}{x}, & \text{ se $x\neq 0$,}\\ 0,& \text{ se $x=0$.} \end{cases} \]
- Justifique a integrabilidade da função $f$, em qualquer intervalo limitado de $\mathbb{R}$.
- Definindo $\Psi(x)=\int_0^{x}f(s)\,ds$, justifique que se trata de uma função diferenciável em $\mathbb{R}$, e calcule $\Psi'(x), x\in\mathbb{R}$.
- Considere a função de variável real definida por $\psi(x)=\int_{x^2}^x \frac{\left|t\right|e^{-t^4}}{1+t^2}\,dt$.
- Calcule os zeros e o sinal de $\psi$;
- Mostre que $\psi(x)\leq \frac{1}{2}\max_{t\in\left[0,1\right]}\log \left(\frac{1+t^2}{1+t^4}\right), \forall_{x\in\mathbb{R}}$.
- (Exercício 6.49 de [2]) Supondo que $f$ é uma função diferenciável em $\mathbb{R}$ e tal que, para qualquer $x\in\mathbb{R}$, $f(x)\lt 0$ e $f'(x)\lt 0$, considere a função $g$ definida em $\mathbb{R}$ por \[g(x)=\int_0^{x^2-4x+3}f(t)\,dt.\]
- Determine os intervalos em que $g$ é monótona, os seus pontos de máximo ou de mínimo e as raizes da equação $g(x)=0$. Estude ainda o sentido da concavidade do gráfico de $g$.
- A função $g$ é majorada? E minorada?
- (Exercício 6.56 de [2]) Considere a função $f(x)=\int_x^{3x} \frac{\cos t}{t}\,dt$.
- Determine o seu domínio e mostre que $f$ é par.
- Mostre ainda que é diferenciável e calcule a sua derivada.
- Mostre que existe $a\gt 0$ tal que $f$ é monótona e limitada em $]0,a[$. Que pode concluir da existência de $\lim_{x\to 0} f(x)$?
- (Exercício 6.51 de [2]) Sendo $\phi(x)=\frac{1-\cos x}{x^2}$, se $x\neq 0$ e $\phi(0)=0$, considere a função $g(x)=\int_0^x\phi(t)\,dt$.
- Justifique que $g$ é ímpar.
- Determine $g'(x)$, para $x\neq 0$ e ainda $g'(0)$.
- Indique as abcissas dos pontos onde o gráfico de $g$ tem tangente horizontal. Justifique que $g$ é estritamente crescente.
- Justifique que $g$ é limitada.
- (Exercício V.14 de [1]) Considere a função $\phi: {]0,+\infty[}\to\mathbb{R}$ definida por \[\phi(x)=\int_1^x \frac{t}{(1+t^2)^2} \log t\,dt.\]
- Calcule $\phi(2)$.
- Mostre que $\phi$ é diferencivel e calcule $\phi'(x)$.
- Estude $\phi$ do ponto de vista do crescimento e mostre que há um só ponto $c\gt 0$ tal que $\phi(c)=0$.
- Seja $\phi:\mathbb{R}\to\mathbb{R}$ definida por \[\phi(x)=\int_{x-1}^{x^2} e^{t^2}\, dt.\]
- Mostre que $\phi$ não é majorada.
- Mostre que $\phi$ possui um ponto de mínimo local no intervalo $]0,1[$.
- Seja \[f(x)=\int_{x-\frac{1}{x}}^{x}te^{-1/t}\, dt.\]
- Mostre que $f$ está definida para $x\in{\left]1,+\infty\right[}$.
Solução
Se $x\gt 1$ então $x-\frac{1}{x}\gt 0$ pelo que o intervalo de integração é da forma $[a,b]$ com $0\lt a\lt b$. Nesse intervalo a função integranda, $te^{-1/t}$ está definida e é contínua e, portanto, é integrável.
- Mostre que o limite $\displaystyle\lim_{x\to 1^+}f(x)$ existe e é um número real no intervalo $\left]0,\frac{1}{2e}\right[$.
Solução
Seja \[\phi(t)=\begin{cases}te^{-1/t}, \text{se $t\gt 0$},\\ 0, \text{se $t=0$.}\end{cases}\] Como $\lim_{t\to 0^+}\phi(t)=\lim_{t\to 0^+}te^{-1/t}=0$, a função $\phi$ é contínua em $[0,+\infty[$ e portanto integrável em qualquer intervalo $[a,b]$ com $0\leq a\leq b$. Da continuidade do integral indefinido, continuidade da função composta e aditividade do integral relativamente ao intervalo de integração obtemos que a função definida para $x\geq 1$ por $\int_{x-\frac{1}{x}}^{x}\phi(t)\, dt$ é contínua valendo no ponto $1$ \[\int_{0}^{1}\phi(t)\, dt=\int_{0}^{1}te^{-1/t}\, dt=\lim_{x\to 1^+} f(x).\] Para estimar este integral usamos que $0\lt te^{-1/t}\lt \frac{t}{e}$ para todo o $t\in {]0,1[}$ donde $0\lt \int_{0}^{1}te^{-1/t}\, dt \lt \int_0^1 \frac{t}{e}\, dt=\frac{1}{2e}$.
- Mostre que $f$ é uma função limitada.
Solução
Notando que a função integranda é crescente e positiva, podemos estimar $f$ para $x\gt 1$ por \[0\lt f(x) \lt \frac{1}{x}x e^{-1/x}= e^{-1/x}\lt 1.\]
- Mostre que $f$ está definida para $x\in{\left]1,+\infty\right[}$.
- Calcule as áreas de cada uma das seguintes regiões do plano:
- $\{(x,y)\in\mathbb{R}^2:x^2\leq y\leq|x|\}$,
- $\{(x,y)\in\mathbb{R}^2:x\geq 0,\ y\geq x,\ y\geq x^3,\ y\leq 4x\}$,
- $\left\{(x,y)\in\mathbb{R}^2: 0\leq y\leq \log x \wedge x\leq a\right\},\;a\gt 1$.
- (Exercício V.11 de [1]) Calcule a área limitada pelas linhas de equações:
- $y=9-x^2$ e $y=x^2$,
- $y^2=4(1-x)$ e $y^2=2(2-x)$,
- $x^2y=1$, $y=-27x$, e $x=-8y$,
- $y=\sqrt[3]{x}$ e $y=\sqrt{x}$,
- $y=\frac{1}{2}x$, $y=x$, e $y=x^2$,
- $y=e^x$, $y=1-x$, $x=1$.
- Calcule a área limitada pela elipse de equação $\frac{x^2}{4}+y^2=1$.
- (Exercício 6.61 de [2]) Calcule a área de região plana definida pelas condições $x^2+y^2\leq 4$ e $y\geq\sqrt{3}x^2$.
- (Exercício 6.62 de [2]) Calcule a área de região do plano limitada pelo gráfico da função $y=\arctg x$ e pelas rectas de equação $ x=1$ e $y=0$.
- Calcule a área da região plana definida pelas condições \[0\leq x\leq \log2 \qquad \text{e}\qquad 0\leq y \leq \dfrac{1}{3-e^x}.\]
- Calcule a área da região do plano limitada pelas linhas de equações $x=y^3$ e $y=x^2$.
Solução
Região limitada por $x=y^3$ e $y=x^2$. \[\int_0^1 \left(\sqrt[3]{x}-x^2\right)\, dx = \left.\left[\frac{3}{4} x^{4/3}-\frac{1}{3} x^3\right]\right|_{x=0}^{x=1}=\frac{3}{4}-\frac{1}{3}=\frac{5}{12}.\]
- Calcule a área da região plana definida por \[ \left\{(x,y)\in\mathbb{R}^2: x\geq 0 \text{ e } \pi-2\arctg x \geq y\geq 2\arctg x\right\}.\]
Solução
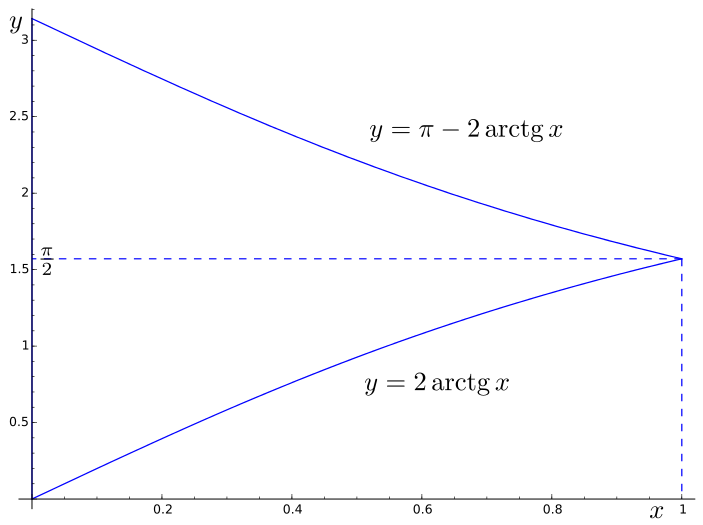
Temos $2\arctg x \leq \pi-2\arctg x \Leftrightarrow \arctg x \leq \frac{\pi}{4} \Leftrightarrow x\leq 1$. Daí que a região pretendida seja a esboçada na figura cuja área é \begin{align*} \int_0^1 (\pi-2\arctg x - 2\arctg x )\, dx & = \pi - 4 \int_0^1 \arctg x \, dx \\ & = \pi - 4\left.\left[x\arctg x \right]\right|_{x=0}^{x=1} + 4 \int_0^1 \frac{x}{x^2+1}\, dx \\ & = 2 \left.\left[ \log(x^2+1) \right]\right|_{x=0}^{x=1} = 2 \log 2 \end{align*}
-
Calcule a área da região do plano definida por \[\left\{(x,y):x\in{\left[0, \frac{\pi}{2}\right[}, \tg x\leq y\leq \sqrt{2}\sen x\right\}.\]
Solução
Os gráficos de $y=\tg x$ e $y=\sqrt{2}\sen x$ para $x\in [0,\pi/2[$. Começamos por notar que, para determinar a região de integração, devemos resolver $\frac{\sen x}{\cos x}\leq \sqrt{2}\sen x$ para $x\in {[0,\pi/2[}$. Como neste intervalo o $\sen$ é não negativo, consideramos a inequação $\frac{1}{\cos x}\leq \sqrt{2}$ com $x\in {[0,\pi/2[}$ que nos conduz a $x\in [0,\pi/4]$.
Assim a área da região é dada por \[\int_0^{\pi/4}(\sqrt{2}\sen x - \tg x)\, dx = \left.[-\sqrt{2}\cos x + \log \cos x]\right|^{x=\pi/4}_{x=0} = -1 + \sqrt{2} +\log(\sqrt{2}/2).\]
- Calcule a área da região limitada pelas linhas de equação $y=\log x$ e $y=\frac{x}{e}\log x$.
Solução
Resolvendo a equação $\log x= \frac{x}{e}\log x\Leftrightarrow \log x \left(1-\frac{x}{e}\right)=0$ obtemos que as duas linhas intersectam-se nos pontos $(x,y)=(1,0)$ e $(x,y)=(e,1)$. Resolvendo a inequação $\log x\gt \frac{x}{e}\log x\Leftrightarrow \log x \left(1-\frac{x}{e}\right) \gt 0$ verificamos que $\log x\gt \frac{x}{e}\log x$ se e só se $x\in{]1,e[}$. Tal permite concluir que a única região limitada do plano que é limitada por estas linhas é $\{(x,y)\in\mathbb{R}^2: x\in[1,e], \frac{x}{e}\log x\leq y\leq \log x \}$.
A região limitada pelas linhas de equação $y=\log x$ e $y=\frac{x}{e}\log x$. Daí que a área pretendida seja dada por \begin{align*}\int_1^e \log x -\frac{x}{e}\log x\, dx & = \left.\left[x\log x \right]\right|^e_1 - \int_1^e 1\, dx - \left.\left[ \frac{x^2}{2e}\log x \right]\right|^e_1 + \int_1^e \frac{x}{2e}\, dx \\ & = e - e + 1 - \frac{e}{2} +\frac{e}{4}-\frac{1}{4e}\\ & = 1 - \frac{e}{4} -\frac{1}{4e}.\end{align*}
- Calcule a área da região \[A=\{(x,y)\in\mathbb{R}^2: x^2\log x \leq y \leq 2x\log x\}.\]
- (Exercício 6.63 de [2]) Calcule a área de região plana consitituída pelos pontos $(x,y)\in\mathbb{R}^2$, que satisfazem as condições seguintes: \[ 0\leq y\leq \frac{\pi}{4},\qquad y\geq \frac{\pi}{16}x^2, \qquad y\leq \arctg x.\]
- (Exercício 6.70 de [2]) Calcule a área da região do plano limitada pelas curvas de equações $y =\log x$, $y=\log^2x$.
- Prove que a área $A$ da região \[ \left\{(x,y)\in\mathbb{R}^2: |x|\leq y \leq e^{-x^2} \right \} \] verifica \[ 0\lt A=2\int_0^\alpha (e^{-t^2}-t)\, dt\lt 1\] em que $\alpha\gt 0$ satisfaz $e^{-\alpha^2}=\alpha$.
Solução
Seja $h:\mathbb{R}\to\mathbb{R}$ definida por $h(x)=e^{-x^2}-|x|$.
Temos que $h(-x)=h(x)$ para todo o $x\in\mathbb{R}$, isto é, $h$ é uma função par.
$h$ é uma função contínua em $\mathbb{R}$ e diferenciável em $\mathbb{R}\setminus\{0\}$.
Temos \begin{align*}h(0) & =1\gt 0, \\ h(1)& = e^{-1}-1\lt 0 \\ h'(x)&=-2x e^{-x^2}-1, \text{ se } x\gt 0\end{align*} o que permite dizer, usando o teorema do valor intermédio no intervalo $[0,1]$ e tomando em consideração o sinal da derivada, que $h$ tem um zero único, que vamos designar por $\alpha$, em $[0,+\infty[$, que $\alpha\in {]0,1[}$ e que $h(x)\geq 0 \Leftrightarrow x\in [-\alpha, \alpha]$.
Portanto \[A=\int_{-\alpha}^\alpha h(x)\, dx= 2\int_0^\alpha h(x)\, dx.\]
Como $\alpha\gt 0$ e $h\gt 0$ em $[0,\alpha[$ temos que $\int_0^\alpha h(x)\, dx \gt 0$.
Por outro lado \[\int_0^\alpha h(x)\, dx \lt \int_0^\alpha 1-x \, dx\lt \int_0^1 1-x \, dx=\frac{1}{2}.\]
A região de área $A$.
Bibliografia
Última edição desta versão: João Palhoto Matos, 10/08/2020 12:04:47.
